Jai Pancholi: Data and It's Applications

Picasso Me - Neural Style Transfer

Neural style transfer is an application of deep learning that provides the ability to apply abstract artistic effects onto ordinary images. First mentioned in "A Neural Algorithm of Artistic Style" by Gatys et al., it is frequently used in mobile phone camera filters, but has yet to achieve much commercial appreciation.

In this article I will explain the mechanism behind style transfers and showcase a open-source implementation applied to an image of my own.

Key Concepts In Deep Learning

What is a (deep) neural network?

Networks, Layers

Neural networks are multi-layer networks of neurons that can learn complex latent patterns in data using labelled training examples.

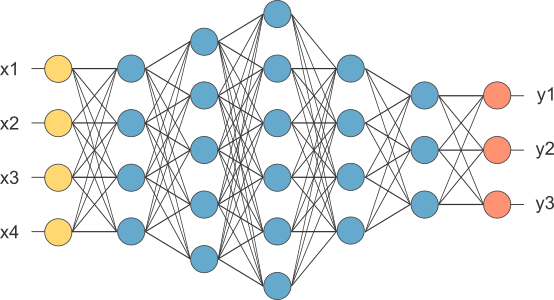
Neural network diagram

The image above is the conventional representation of a deep neural network. This network consists of an input layer (yellow), an output layer (red), and hidden layers (blue). When the number of hidden layers is not small, say greater than 3, these networks are considered deep neural networks.

Neurons, Activation Functions

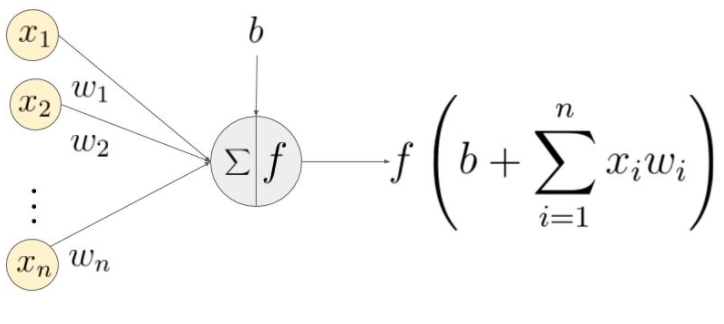
What happens in a neuron

The diagram above is a diagram of the mechanics of each neuron. The key information that each neuron contains are weights and biases. These weights and biases are applied to all input numbers, this intermediate value is given to an activation function that squeezes the number between 0 and 1 and this output and released back into the network. Activation functions come in a few popular flavours: step, tanh, sigmoid, rectified linear unit (ReLU), and leaky ReLU.

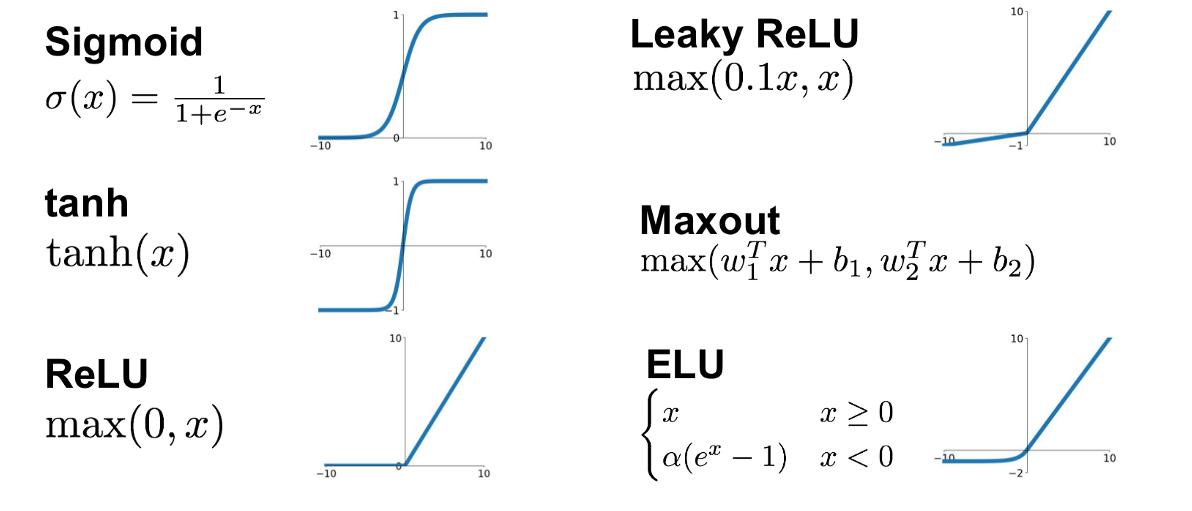
Activation functions

Cost/Loss Functions

When we build a network, the network tries to predict the output as close as possible to the actual value. We measure this accuracy of the network using the cost/loss function. The cost or loss function tries to penalize the network when it makes errors.

In fact, a neural network with a single hidden neural network and with the sigmoid activation function and log loss cost function is actually the traditional logistic regression.

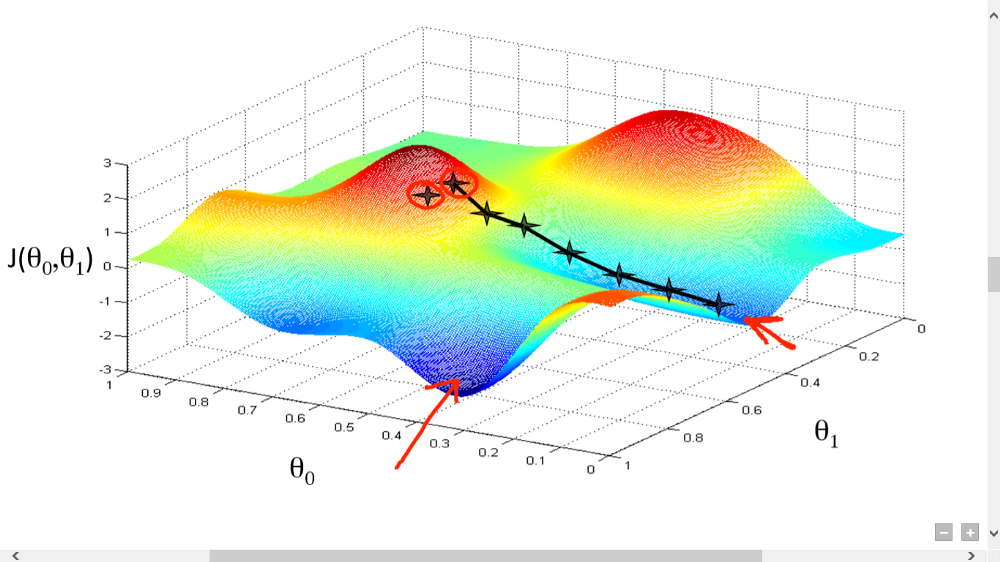
3-d map of the loss function

Gradient Descent, Forward Propagation, Backpropagation

The plot above is an example of the mapping of cost of the network against all of the network weights and biases. A network 'learns' by reducing the cost function to its most minimal point by changing the weights and biases in each of the neurons of the network. The network learns quickest by changing weights such that the decrease in cost is quickest, going down the steepest gradient of the cost function: this is called gradient descent.

The overall mechanics of a learning step (epoch) of a neural network is as follows:

1. Randomise weights and biases

2. Forward propagate the input data, through all of the neurons and generate output values and associated costs.

3. Backward propagate through the network by performing gradient descent to learn which direction to shift weights and biases in the most optimal way.

4. Update the weights and biases of each neuron

5. Repeat steps 2-4 until a certain condition has been met.

Once the above steps are complete, we have a trained neural network! To learn more about the nuances of neural networks I recommend taking the Deep Learning Specialisation on Coursera.

What is a convolutional neural network?

Convolutional networks are types of neural networks that work very well with large observation sizes. They are primary choice for any system that involves image data. Images can be represented to a 3-dimensional matrix with width and length determined by the size in pixels of the image, and the depth of the matrix represents the 3 colour channels in an RGB image. It follows that since image sizes can be fairly large, the number of parameters (weights and biases) in a neural network can get very large, and therefore very computationally expensive to train.

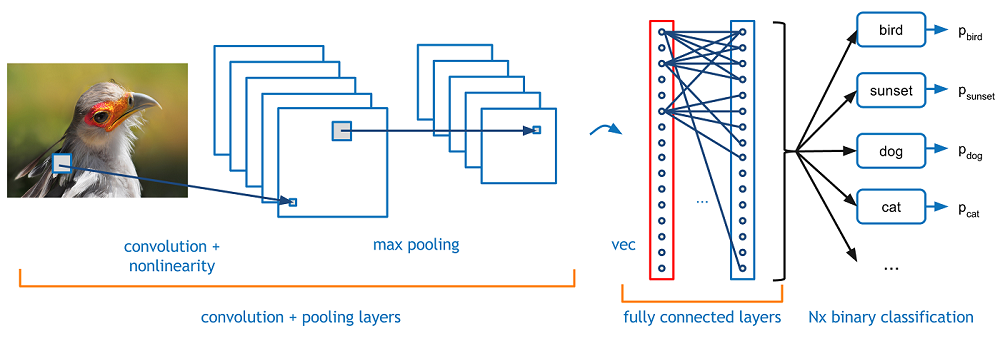
How convolutions work

A solution to this is a convolutional neural network. A convolutional network is a neural network that has convolutional layers. A convolutional layer swaps out weights and biases for a set of n x n matrixes, called filters, that apply a dot product with the input across sliding windows of the image. For more information on what sliding windows are I suggested reading my blog post on face detection. To learn more about the key concepts of CNNs such as padding, max pooling, check out.

What are convolutional neural networks learning?

Before I talk specifically about neural style transfer, I want to showcase an interesting visualisation of the features that convolutional neural layers are learning.

In general, the first few layers of networks typically learn simple patterns in the data, and deeper layers unearth more complex structures. This phenomena can be shown clearly in convolutional where we can identify parts of images that trigger each filter of each layer the most. The following diagram, taken from the paper "Visualizing and Understanding Convolutional Networks" shows a convolutional network, which has been trained on ImageNet, a open dataset of 1.3 million images, spread over 1000 different classes, and gives a great visualisation on features that are learnt.

What do CNNs actually learn?

The first layer is able to detect edges and colours, the second layer can learn textures and circular objects. Layer 5 is able to detect dog faces and the petals of a flower.

Application: Neural Style Transfer

Touching on Theory

Slide from Deep Learning, Andrew Ng, Coursera

Neural style transfer is a novel application of convolutional neural networks with the key points:

▴ The inputs are a content image C (i.e. an ordinary photograph) and a style image S (i.e. an artsy painting)
▴ The output is another image, G
▴ The pixels in the generated image G are the parameters that the model learns
▴ The cost function consists of a linear combination of a content cost function and a style cost function, which take in the (content image, generated image) and (style image, generated image) in as arguments, respectively.

Style transfer loss function

Code

There are many open source implementations of neural style transfer - all of the ones I have discovered seem to use the VGG network's pretrained weights, and perform gradient descent using the updated style transfer cost function. You can find an example from the Keras documentation, this Towards Data Science post, or this Git repository.

I use the final example as an implementation for neural style transfer. I initially tried to run an optimisation process on my laptop (2019 Macbook Pro 13", 1.4Ghz quad core i5, 8GB ram) but quickly realised it was a horrendously slow process. It was taking ~30 minutes 10 iterations of the model, or around 200 seconds per iteration. I then decided to try out Google Colab, a cloud version of Jupyter notebook that allows you to train on GPUs or TPUs; this massively improved the speed and I was able to complete 1,000 iterations in less than 5 minutes. What's more, you are able to mount your personal Google Drive into whatever instance of Google Colab Notebook you use, and therefore easily store images / code and access these through interactive interface of the notebook.

Below are a few tests of the transfer process completed on a picture I took during my recent trip to Rome. The results are quite impressive, even without much hyperparameter tuning.